气基直接还原炼铁的能耗问题

2022-08-29 作者：佚名网友评论 0 条

为了提高气基直接还原炼铁过程中气体的利用率，降低综合能耗，本文从单一气体和混合气体还原铁氧化物理论模型出发，采用化学平衡法和最小自由能法分别计算气体的逐级还原气体利用率和综合还原气体利用率

孙贯永^{1, 2}，郭汉杰^{1, 2}，李彬^{1, 2}

1．北京科技大学冶金与生态工程学院

2．高端金属材料特种熔炼与制备北京市重点实验室

根据世界钢铁协会发布的《世界钢铁统计数据2019》[1]，过去三年里，全球直接还原铁产量增长迅猛，2016年全球直接还原铁产量约7590万吨，2017年约8870万吨，2018年约9980万吨，增长率分别为16.86%，12.51%。气基直接还原的工艺，占世界还原铁总产量的80%以上，具有投资少，单体规模大，污染排放低等优势。我国的气基直接还原铁产量虽然当前为零，但是众多企业和科技工作者正在努力开发适用中国条件的工艺和方法。

还原气利用率和综合还原能耗直接关系气基直接还原工艺开发的成败，前者是限定了气体利用限度，后者决定了生产成本的高低。

本文针对气体还原铁氧化物的气体利用率和能耗，从气体还原炼铁的热力学数据出发，建立气体还原的能耗模型，分析了吨金属铁生产所需的还原气量和热能量，对还原气体的选择和搭配、还原铁生产的节能降耗、还原工艺条件的改善都具有一定的参考意义。

1 气体还原铁氧化物模型

1.1 单一气体还原铁氧化物

1.1.1 还原气消耗量

根据化学平衡法原理，依据热力学手册数据手册[1]，计算单一气体还原铁氧化物的利用率。

已知，当温度大于570℃，Fe2O3的还原分为三个阶段逐级进行，依次为：Fe2O3→Fe3O4，Fe3O4→FeO，FeO→Fe。

表 1列出单一气体还原铁氧化物的化学方程式和相应的热力学函数数值。表中，、，分别式是化学反应在273.15K时标准摩尔熵变、标准摩尔焓变，单位分别为J•K-1•mol-1，kJ•mol-1。还原反应的吉布斯自由能变根据物质标准生成吉布斯自由能求得，然后对开尔文温度T做线性拟合，得到的线性关系式。结合等温方程式，可以求得还原反应的平衡常数。的关系如下式所示：

已知1 mol CO或1 mol H2还原铁氧化物中1 mol O生成1 mol CO2或1 mol H2O，根据不同阶段的还原失氧量计算该阶段还原气消耗量，则三个阶段的还原气CO或H2消耗量依次为67 m3•tFe-1，133 m3•tFe-1，400 m3•tFe-1。当以赤铁矿/氧化球团、磁铁矿、方铁矿（铁氧化物氧铁物质的量比=0.87～0.95）为原料生产1t金属Fe时（CO+H2）还原气消耗量，分别为600 m3•tFe-1、533 m3•tFe-1、421～460 m3•tFe-1。

当采用混合气体（CO+H2）还原铁氧化物，不可避免的要发生水煤气反应，化学方程式和热力学函数如下所示：

当温度大于1104.206（831.056℃）时，该反应逆向进行；反之，反应正向进行。无论水煤气向何方向进行，都会改变还原气中CO或H2的浓度，进而影响CO和H2对铁氧化物的还原。

1.1.2 标况气体利用率

从铁氧化物逐级还原反应方程式式～式，式～式可以看出，单一还原气体的化学反应是均相反应，反应前后气体的体积不变。当以纯CO或纯H2为初始还原气体时，反应的标准平衡常数可以通过浓度比的方式表达，如式和式所示，进而可用标准平衡常数表达还原气体在标况下的利用率和标况下平衡浓度，如式、和式、所示。

式中，分别为纯CO或纯H2为初始还原气体时，反应达到平衡时气体组元i的分压和浓度；，分别为CO和H2的标准平衡常数；，分别为纯CO和纯H2还原铁氧化物的标况利用系数；，为标准大气压，101.325kPa。

在800～950℃温度范围内，通过式、式、式，可以求得标况气体利用率与温度的关系，如图 1所示。

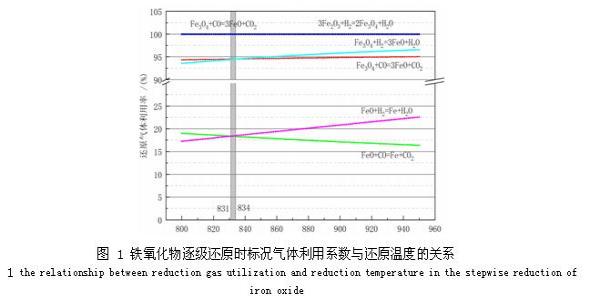
从图1可以看出，在800～950℃范围内，Fe2O3→Fe3O4、Fe3O4→FeO、FeO→Fe逐级还原过程还原气体利用率逐级减小，分别为100%，93.57%～ 96.57%，16.35%～22.54%。温度对于第一级还原反应Fe2O3→Fe3O4的影响几乎没有。温度对于第二级还原反应Fe3O4→FeO的影响比较小，气体利用率在微小上下区间内变化。温度对于第三级还原反应FeO→Fe的影响比较大，气体利用率随温度的变化斜率明显大于第二级还原反应。

另外，对于第二、三级还原反应，CO气体利用率随温度的升高而减小，H2气体利用率随温度的升高而增大。在831～834℃范围时，CO和H2还原相同铁氧化物的气体率相等。高于该温度范围，还原相同铁氧化物的利用率H2高于CO，且随着温度增大，两者的差距也随之变大；低于该温度范围，还原相同铁氧化物的利用率H2低于CO，且随着温度增大，两者的差距随之变小。

1.2混合气体还原铁氧化物

根据最小自由能原理，依据热力学手册数据手册[1]，计算混合气体还原铁氧化物的平衡组成和气体还原气利用率。

1.2.1 最小自由能原理

将气基直接还原炼铁过程看作是一个封闭体系，进料为氧化球团矿和还原混合气，出料为金属铁、脉石、尾气，化学反应在高温下充分进行而达到平衡状态。对于这一气固反应的多元多相体系，当体系达到热力学平衡时，总的自由能最小。

最小自由能原理可以从体系中组元的始态和终态的角度来考虑体系的平衡问题，通过初始态，计算平衡态，根据终止态与起始态的物质的量变化，可以判断复杂体系中特定组元的化学反应量。其模型如下式所示，式为约束条件。

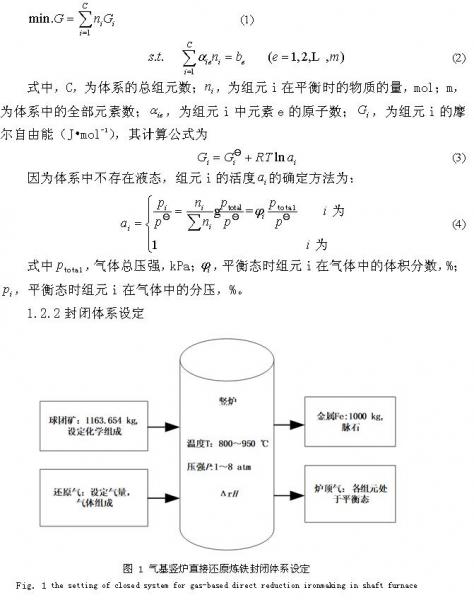
气基竖炉直接还原炼铁封闭体系的设定，不考虑气体通过球团散料层的压降，只考虑体系化学平衡和热焓变化。可以认为在封闭体系内物质在起始态和终止态的温度都等于还原温度，则体系的热焓变化ΔrH，就是体系内化学反应的焓变之和，也就是生成物的标准生成焓变减去反应物的标准生产焓变，即

式中，i，表示生成物，j，表示反应物；，表示增加的生成物的物质的量，mol;，表示减少的反应物的物质的量；，，分别表示物质i，j的标准摩尔生成焓，kJ•mol-1。

进料和出料物质组成设定为：

初始态：Fe2O3（s），H2（g），CO（g），H2O（g），CO2（g），N2（g）；

终止态物：Fe2O3（s），Fe3O4（s），FeO（s），Fe（s），H2（g），CO（g），H2O（g），CO2（g），N2（g）。

（s），（g），分别表示物质为固态、气态。需要注意的是，脉石包含在初始态和终止态中，因为不参与化学反应，且固态物质的活度为1，因此在作最小自由能计算时，不考虑脉石；而N2虽然不参与化学反应，但是N2的存在影响其他气体的浓度，因此，包含在最小自由能计算中。因此，体系总元素数m=5，分别为Fe、O、C、H、N；总组元数C=9，即终止态所列出的9种可能存在物质。

设定初始还原气体量、气体组成。

设定还原温度设定为800～950℃，设定气体总压为101.325kPa。

由于还原气组成与还原气最小需求量之间有着直接的关系，而生产中还原气通常采用过量的方式保证金属化率，因此本计算中不以最小还原气量为依据计算还原反应平衡组成和体系焓变，而是设定一个较大值。因为在还原气中引入了CO2、H2O、N2等非还原气体，还原气的利用率将更低，而吨铁还原气消耗量不变。因此，还原气量取较大值，用于最小自由能计算，以研究混合气体中利用率和吨铁还原能耗等规律。

根据式和式，已知物质的标准吉布斯自由能，温度T，总压，球团质量和化学组成，混合还原气体积和气体组成，可以求得相应条件下平衡态时各物质的量。具体计算式如下所示：